LIS (Longest Increasing Subsequence) 최장 증가 부분 수열
최장 증가 부분 수열은 말 그대로 가장 길게 증가하는 부분 수열으로
즉, 어떤 수열에서 만들 수 있는 부분 수열 중에서 가장 길면서 오름차순을 유지하는 수열을 LIS라고 합니다.
좀 더 이해하기 쉽도록 아래 그림을 봅시다.

만약 위와 같은 배열이 있을 때 만들수 있는 증가 부분 수열은 위와 같으며
최장 증가 부분 수열은 만들 수 있는 증가 부분 수열 중 길이가 가장 긴 [1, 2, 6]이 됩니다.
LIS를 구현하는 방법으로는 두가지가 있습니다.
- DP
[알고리즘] 동적 프로그래밍 (DP) 란? feat.동적 계획법
동적 프로그래밍(Dynamic programming) 란? 동적 프로그래밍은 "큰 문제"를 "부분 문제"로 나누고, "부분 문제"의 정답으로 "큰 문제"의 답을 찾는 알고리즘 설계 기법입니다. 동적 프로그래밍의 대표적
hstory0208.tistory.com
- 이분 탐색
[알고리즘] Binary Search(이진 탐색/이분 탐색)이란?
Binary Search(이진 탐색/이분 탐색) 이진 탐색 알고리즘은 정렬되어 있는 배열에서 찾고자 하는 특정한 값을 찾아내는 알고리즘입니다. 이진 탐색 알고리즘이 탐색하는 방식은 배열의 중간에 있는
hstory0208.tistory.com
DP를 활용한 LIS 구현
DP를 활용할 시 이중 반복문을 사용하여 O(n^2)의 시간 복잡도를 가집니다.
그렇기에 입력 값의 크기가 작을 경우에 유용합니다.
DP를 이용한 방식
i번째 원소와 이전 원소들의 비교하며 원소들 중에서 i번째 원소보다 작은 원소들 중 DP값이 가장 큰 값에 + 1을 하여 dp[i]의 값을 구합니다.
import java.util.Arrays;
public class LIS_DP {
public static void main(String[] args) {
int arr[] = {3, 2, 4, 1, 6};
int dp[] = new int[arr.length];
dp[0] = 1; // LIS의 첫 번째는 항상 1이다.
for (int i = 1; i < arr.length; i++) {
// 첫 원소부터 i원소 전까지 비교
for (int j = 0; j < i; j++) {
if (arr[j] < arr[i]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
// 증가 부분 수열의 길이는 1부터 시작하므로 0인 값을 1으로 변경해준다.
if (dp[i] == 0) {
dp[i] = 1;
}
}
}
System.out.println("arr : " + Arrays.toString(arr));
System.out.println("DP : " + Arrays.toString(dp));
}
}

LIS DP 과정

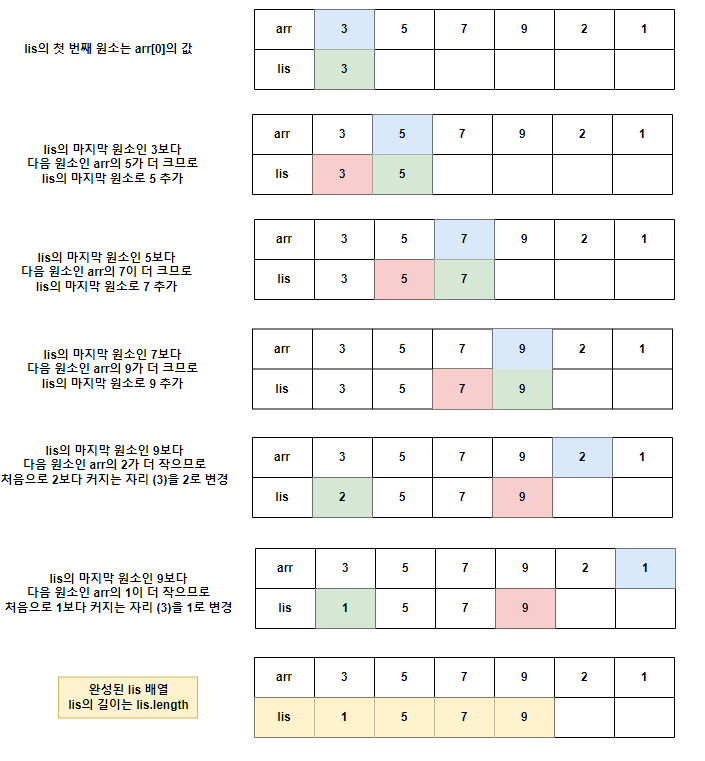
이분 탐색을 활용한 LIS 구현
이분 탐색을 활용할 시 O(logn)의 시간 복잡도를 가집니다.
입력 값이 크기가 클 경우 DP를 활용하면 효율이 떨어지기 때문에 이분 탐색을 활용하여 시간 복잡도를 줄일 수 있습니다.
또한 이분 탐색을 활용하는 경우에는 정확한 LIS가 아닌 LIS의 길이를 구할 때 사용됩니다.
import java.util.Arrays;
public class LIS_Binarysearch {
public static void main(String args[]) {
int[] arr = {3, 5, 7, 9, 2, 1, 4, 8};
int size = arr.length;
System.out.println("arr : " + Arrays.toString(arr));
System.out.println("LIS 길이 : " + binarySearch(arr, size));
}
public static int binarySearch(int[] arr, int size) {
int[] lis = new int[size + 1]; // 가장 긴 증가하는 부분 수열. 가장 뒤에 있는 값은 부분 수열 중 가장 최댓값
int start = 0;
lis[start++] = arr[0]; // lis[start] 값을 arr[i]로 변경하고 1증가시킨다.
for (int i = 1; i < size; i++) {
// lis값의 맨 마지막 원소가 arr[i] 보다 작을 경우
if (lis[start - 1] < arr[i]) {
lis[start++] = arr[i]; // 해당 원소를 arr[i]값으로 변경하고 start를 1 증가 시킨다.
} else {
int end = 0;
while (start <= end) {
int mid = start + (end - start) / 2;
if (arr[mid] == arr[i]) {
return mid;
}
if (arr[mid] < arr[i]) {
start = mid + 1;
}
if (arr[mid] > arr[i]) {
end = mid - 1;
}
}
// start < end 일 경우 lis[start]의 값은 arr[i]의 값이 된다.
lis[start] = arr[i];
}
}
return start;
}
}
LIS 이분 탐색 과정
'◼ CS 기초 지식 > [알고리즘]' 카테고리의 다른 글
| [알고리즘] 라인 스위핑 (Sweeping) (0) | 2023.02.01 |
|---|---|
| [알고리즘] 투 포인터(Two Pointers)란? (0) | 2023.01.27 |
| [알고리즘] 힙 정렬(Heap Sort)이란? (0) | 2023.01.21 |
| [알고리즘] Binary Search(이진 탐색/이분 탐색)이란? (0) | 2023.01.20 |
| [알고리즘] 완전탐색(Exhaustive search)이란? (0) | 2023.01.19 |