반응형
투 포인터(Two Pointers)
투 포인터는 말 그대로 두 개의 포인터를 사용하여 문자열, 배열, List에서 원하는 값을 찾는 것 입니다.
투 포인터를 활용하기 위한 조건은 주어진 배열에서 연속된(정렬이 아닌) 부분 배열을 통해 문제를 해결할 수 있어야 합니다.
투 포인터 알고리즘을 활용하는 대표적인 예로는 배열에서 특정한 합을 갖는 부분 연속 수열을 찾을 때가 있습니다.
만약 이중 반복문을 통해 부분 연속 수열을 찾는다면 O(n^2)의 시간복잡도가 소요되는 반면
투 포인터를 활용한다면 O(n)의 시간복잡도로 시간을 단축 시킬 수 있습니다.
투 포인터는 두 개의 포인터를 사용하기 때문에 두 개의 인덱스를 가르키는 변수가 필요합니다.
그 변수를 하나는 "시작점을 가르키는 start", 다른 하나는 "끝점을 가르키는 end"가 있다고 했을 때
처음에 start와 end는 인덱스 0에서 시작하고, start <= end를 만족해야합니다.
현재 부분합 "sum"이 찾고자 하는 값 "findValue" 보다 작다면 (sum < findValue), end번째의 값을 sum에 더한 뒤 end의 인덱스를 1 증가시킵니다.
현재 부분합 "sum"이 찾고자 하는 값 "findValue" 보다 크거나 같다면 (sum >= findValue), start번째의 값을 sum에서 뺀 뒤 start의 인덱스를 1 증가 시킵니다.
투 포인터 예제 코드 (배열에서 특정한 합을 갖는 부분 연속 수열의 개수 찾기)
import java.util.Arrays;
public class TwoPointer {
public static void main(String[] args) {
int[] arr = {1, 3, 2, 5, 4};
Arrays.sort(arr);
System.out.println(twoPointCount(arr));
}
private static int twoPointCount(int[] arr) {
int count = 0, end = 0,start = 0, sum = 0;
int findValue = 5;
while (true) {
// 부분합이 찾는 값보다 크거나 같다면
if (sum >= findValue) {
// 부분합이 찾고자하는 값과 같다면 count + 1
if (sum == findValue) {
count++;
}
sum -= arr[start++]; // 현재 start 위치의 값을 빼고 start + 1
// 배열의 길이를 넘어간다면 종료.
} else if (end == arr.length) {
break;
// 부분합이 찾는 값보다 작다면, 현재 end 위치의 값을 더하고 end + 1
} else if (sum < findValue) {
sum += arr[end++];
}
}
return count;
}
}
투 포인터 파이썬 예제 코드
import sys
input = sys.stdin.readline
findValue = 5
nums = [1, 3, 2, 5, 4]
sum = 0 # 부분합
start = 0
end = 0
cnt = 0
while True:
# 현재 부분합이 찾고자하는 값보다 크거나 같다면
if sum >= findValue:
if sum == findValue:
cnt += 1
sum -= nums[start]
start += 1
# 현재 부분합이 찾고자하는 값보다 작다면
elif sum < findValue:
if end == len(nums): # 배열의 끝까지 탐색했다면 종료
break
sum += nums[end]
end += 1
print(cnt)
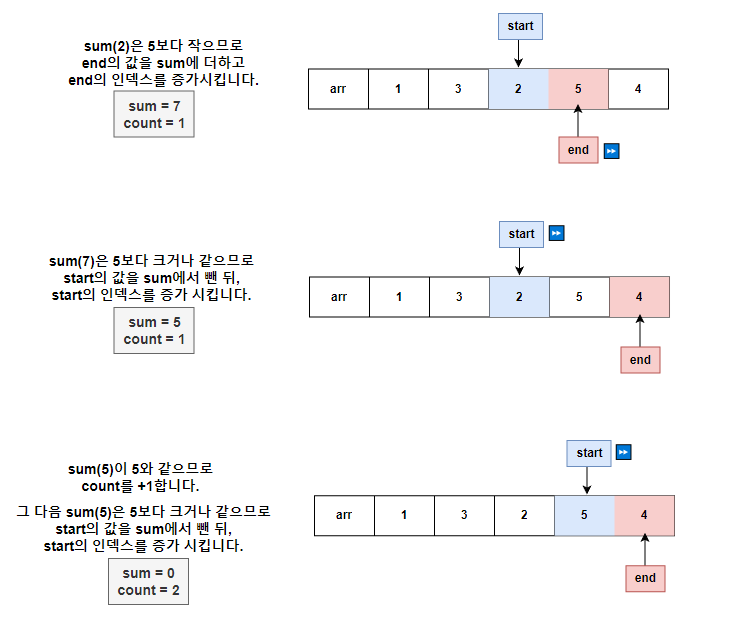
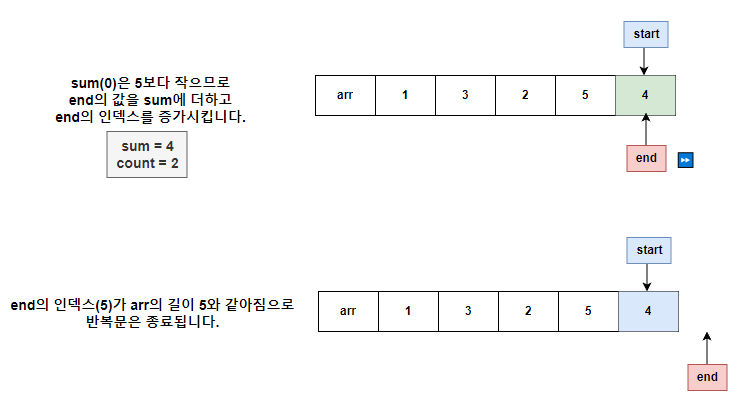
탐색 과정
위의 코드대로 투 포인터가 탐색하는 과정을 그림을 통해 설명하였습니다.


'◼ CS 기초 지식 > [알고리즘]' 카테고리의 다른 글
| [알고리즘] 다익스트라(Dijkstra) - 최단거리 알고리즘 (0) | 2023.02.01 |
|---|---|
| [알고리즘] 라인 스위핑 (Sweeping) (0) | 2023.02.01 |
| [알고리즘] LIS(최장 증가 부분 수열)이란 ? (2) | 2023.01.26 |
| [알고리즘] 힙 정렬(Heap Sort)이란? (0) | 2023.01.21 |
| [알고리즘] Binary Search(이진 탐색/이분 탐색)이란? (0) | 2023.01.20 |